Home

Exploratory Analysis of Distribution



In this section, we'll take a closer look at the distribution of various columns in our bank churn dataset. Utilizing Python code, we'll examine key variables such as credit scores, ages, account balances, and product usage. This analytical approach allows us to uncover patterns and insights that go beyond raw numbers, providing a clear understanding of customer behaviors and setting the foundation for informed decision-making.

							
	import csv
	import pandas as pd
	import matplotlib.pyplot as plt
	import seaborn as sns
	
	# Load Data
	filename = 'data/BankCustomerChurnPrediction.csv'
	data = pd.read_csv(filename)
	df = pd.DataFrame(data)
	pd.set_option("display.max_columns", None)
	pd.set_option("display.max_rows", None)
	
	# Initial data exploration + null value check
	print(df.isnull().sum())
	""">> customer_id         0
	credit_score        0
	country             0
	gender              0
	age                 0
	tenure              0
	balance             0
	products_number     0
	credit_card         0
	active_member       0
	estimated_salary    0
	churn               0
	"""
	
	# Check the amount of columns and rows
	print(df.shape)
	# >> (10000, 12)
			
	print(df.info())

	print(df.describe())
	
	# Cursory glance at snippet of table
	print(df.head(15))
	
	# Complete list of column names
	with open(filename) as f:
		reader = csv.reader(f)
		header_row = next(reader)
	print(header_row)


	# Check the headers of columns
	print(df.columns)
	"""Index(['customer_id', 'credit_score', 'country', 'gender', 'age', 'tenure',
	'balance', 'products_number', 'credit_card', 'active_member',
	'estimated_salary', 'churn']"""



This dataset is already cleaned and contains no missing values or duplication. It is ready for basic views of it's distribution. Provided below is an example of the code needed to visualise the distributions of important variables using Matplotlib. 


						
	# Visualisation of data
	# Age Histogram
	plt.hist(df['age'], bins=20, color='skyblue', edgecolor='black')
	plt.xlabel('Age')
	plt.ylabel('Count')
	plt.title('Distribution of Age')
	plt.show()
	
	# Gender bar Graph
	plt.figure(figsize=(8, 6))
	sns.countplot(x='gender', data=df, palette='pastel')
	plt.title('Distribution of Gender')
	plt.show()
	
	# Country plot
	plt.figure(figsize=(8, 6))
	sns.countplot(x='country', data=df, palette='pastel')
	plt.title('Distribution of Country')
	plt.show()



Some of the more interesting resulting distributions are provided below.

distribution_of_ages dist_gender

dist_balance dist_country

dist_credit dist_salary

As this data is looking at banking customers and products, its important to consider how this may impact the distributions observed. These distributions indicate a mostly male population from Europe between the ages of 30-40. Our data also indicates a skewed distribution towards a better credit score.








Relational Analysis

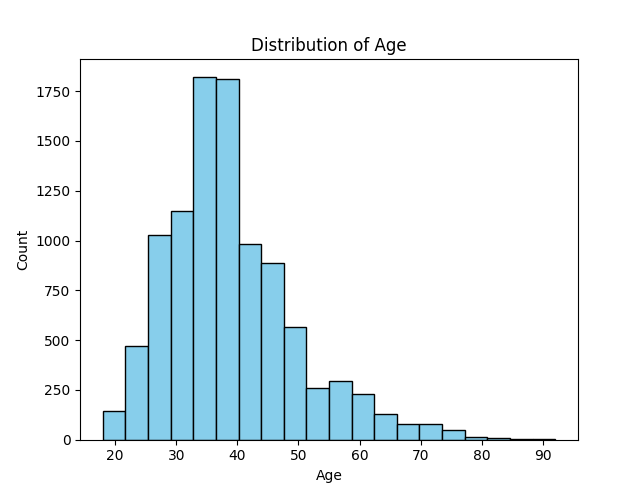
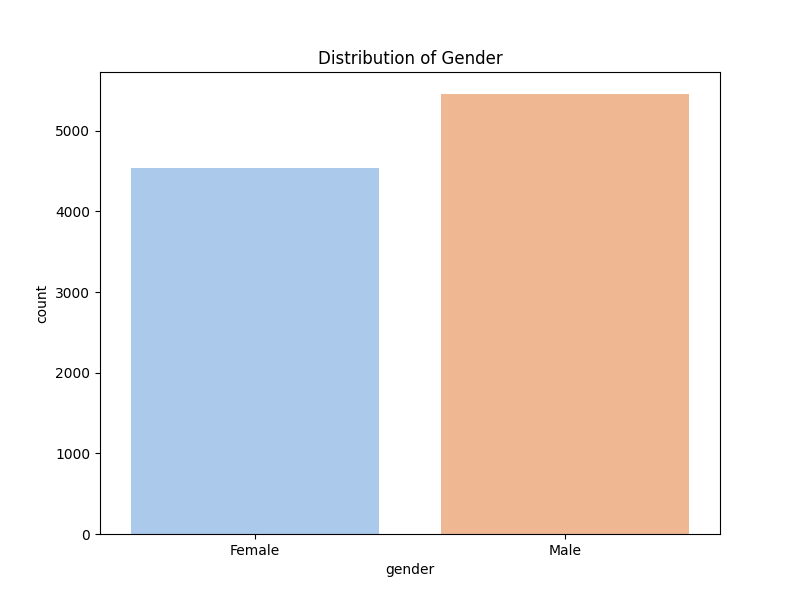
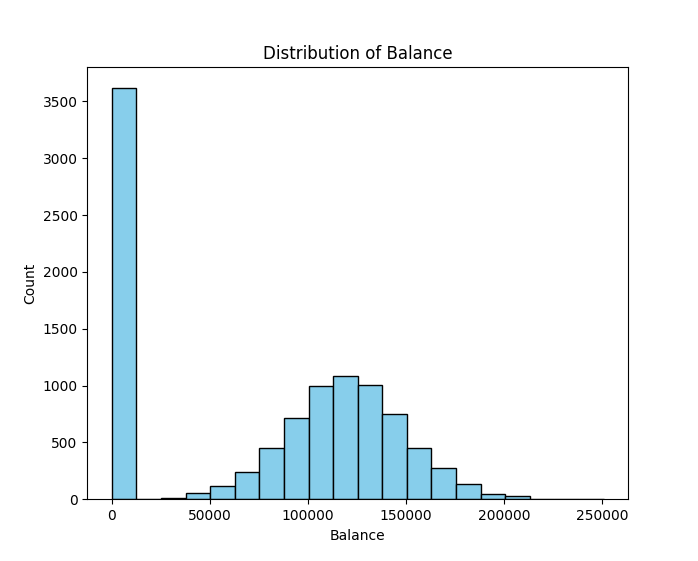
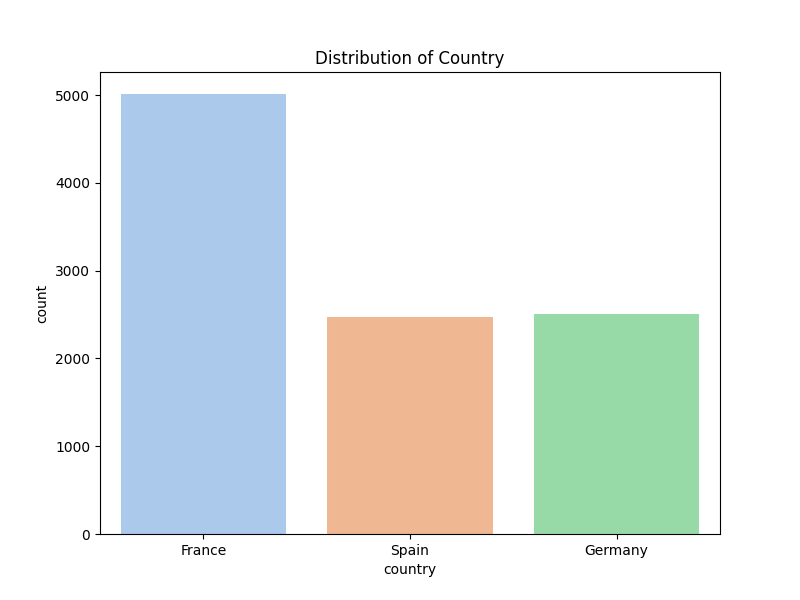
The following section continues to visualise our bank customer data through comparing those who churned vs didnt.







To better understand what features predict a higher likelihood of customer attrition. Correlation and distribution were further examined using the following python and more.

						
	# Stacked bar plot for Number of Products vs. Churn
	products_churn_cross = pd.crosstab(index=df['products_number'], columns=df['churn'])
	products_churn_cross.plot(kind='bar', stacked=True, color=['lightblue', 'salmon'])
	plt.title('Churn by Number of Products')
	plt.xlabel('Number of Products')
	plt.ylabel('Count')
	plt.show()
	
	
	# Cross-tabulation
	gender_churn_cross = pd.crosstab(df['gender'], df['churn'])
	plt.figure(figsize=(8, 6))
	gender_churn_cross.plot(kind='bar', stacked=True, color=['lightblue', 'salmon'])
	plt.title('Churn by Gender')
	plt.xlabel('Gender')
	plt.ylabel('Count')
	plt.show()
	
	# Stacked bar plot for Gender and Credit Card vs. Churn
	gender_credit_churn_cross = pd.crosstab(index=[df['gender'], df['credit_card']], columns=df['churn'])
	gender_credit_churn_cross.plot(kind='bar', stacked=True, color=['lightblue', 'salmon'])
	plt.title('Churn by Gender and Credit Card')
	plt.xlabel('Gender, Credit Card', rotation=0)  # Rotate x-axis labels to be horizontal
	plt.ylabel('Count')
	plt.show()
	
	# Heatmap for selected numerical variable correlations
	plt.figure(figsize=(10, 8))
	selected_numerical_cols = ['age', 'balance', 'products_number', 'estimated_salary']
	selected_corr_matrix = df[selected_numerical_cols].corr()
	sns.heatmap(selected_corr_matrix, annot=True, cmap='coolwarm')
	plt.title('Correlation Matrix for Selected Numerical Variables')
	plt.show()









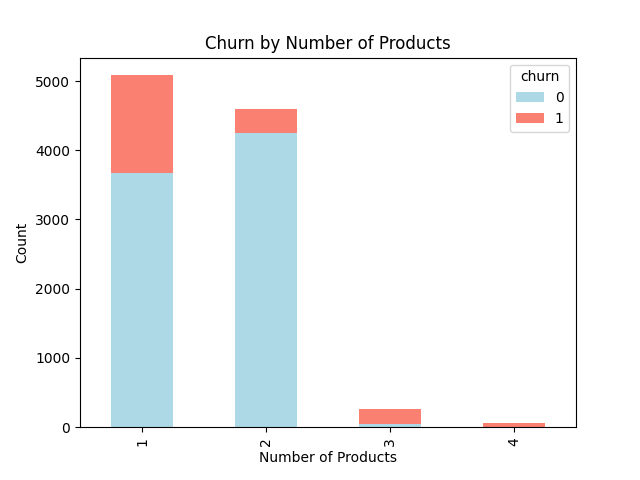
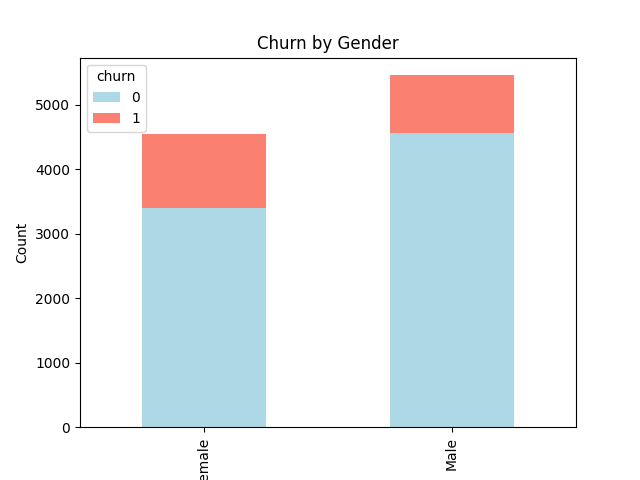
The following bar graphs show an increased likelihood of attrition among customers who use more than 2 products and females.

churn_product gender_churn





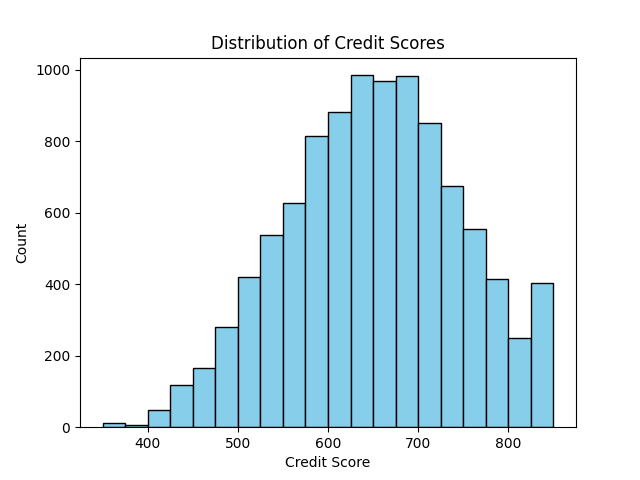
Looking more closely at distribution of tenure and credit score, its plausible that the newest customers and oldest customers have an increased likelihood of attrition, seen through a much larger interquartile range. No significant differences between customers who have churned and haven't were seen when investigating credit scores.

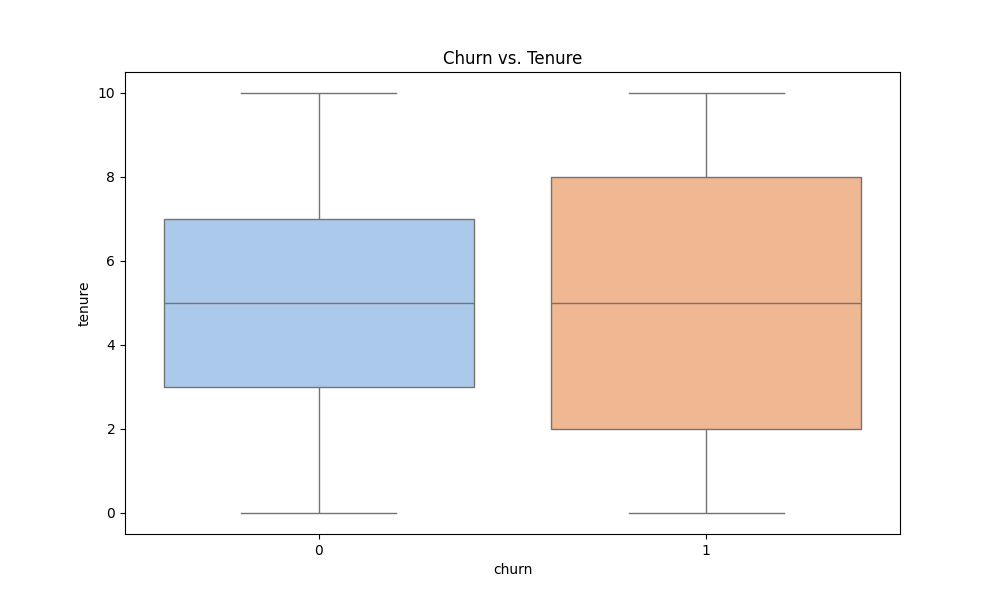
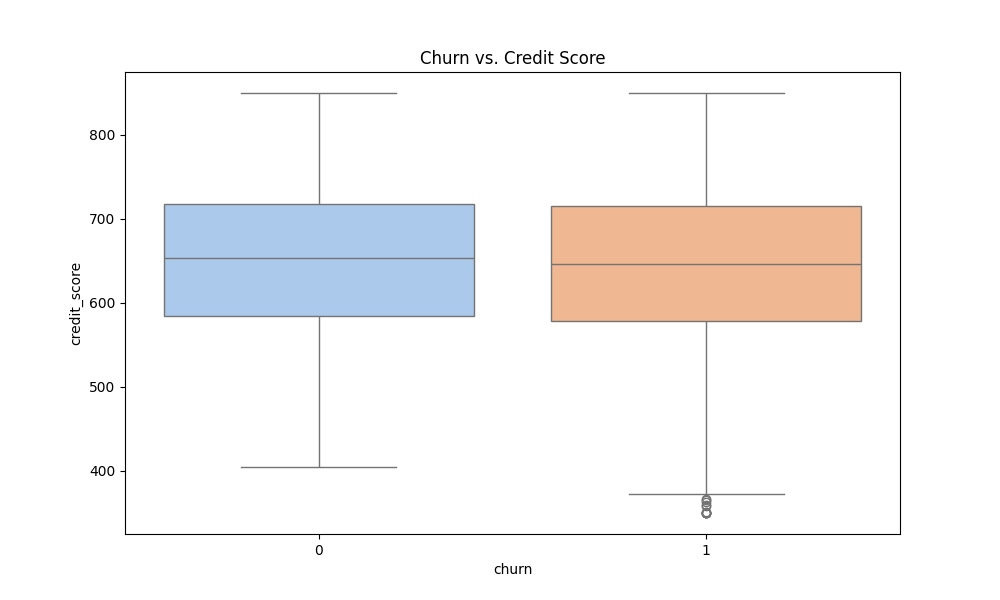
churnvstenurebox churnvscreditbox

While comparing churn versus no churn in these variables can reveal crucial distinctions, the effectiveness of this analysis is enhanced by incorporating additional demographic variables. Let's revisit credit scores and tenure. Below is the code used for more comprehensive visualizations.

						

	# Distribution of Credit Scores for Churned and Not Churned customers
	plt.figure(figsize=(12, 6))
	sns.kdeplot(df[df['churn'] == 0]['credit_score'], label='Not Churned', shade=True)
	sns.kdeplot(df[df['churn'] == 1]['credit_score'], label='Churned', shade=True)
	plt.xlabel('Credit Score')
	plt.ylabel('Density')
	plt.title('Distribution of Credit Scores by Churn')
	plt.legend()
	plt.show()
	
	# Scatter plot of Tenure vs. Age with Hue by Churn
	plt.figure(figsize=(12, 8))
	sns.scatterplot(x='tenure', y='age', hue='churn', data=df, palette='coolwarm', alpha=0.7)
	plt.title('Scatter Plot of Tenure vs. Age with Hue by Churn')
	plt.xlabel('Tenure')
	plt.ylabel('Age')
	plt.show()

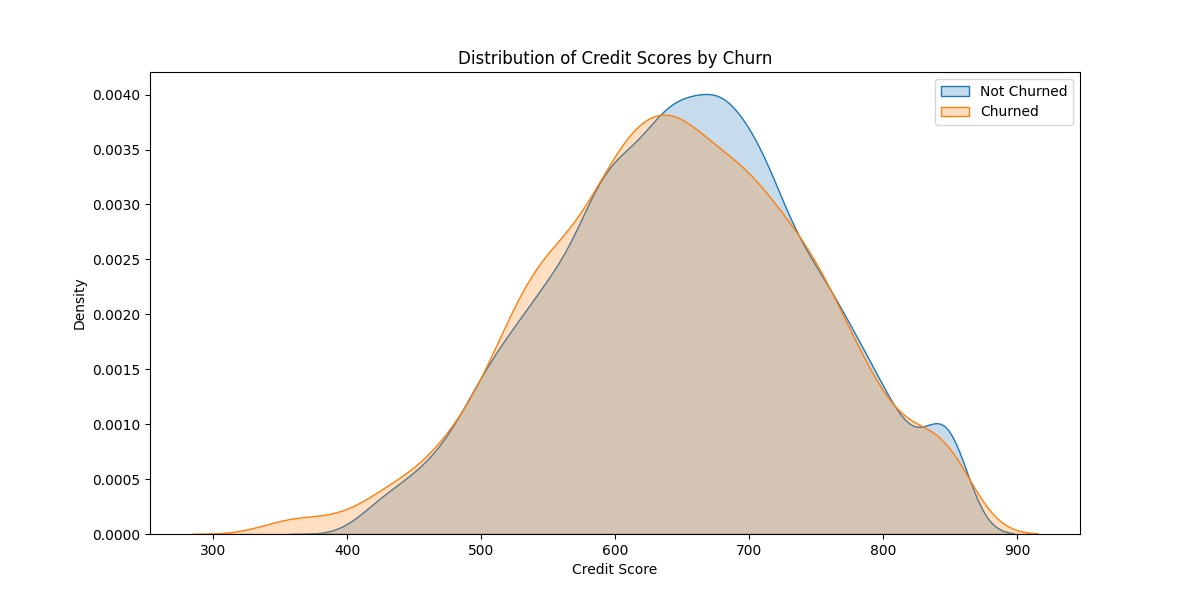
creditchurnvsnochurn
Looking at distribution in this way shows a subtle but potentially significant difference in credit scores of those who are churned, indicating a lower credit score is more associated with customers leaving the bank. .


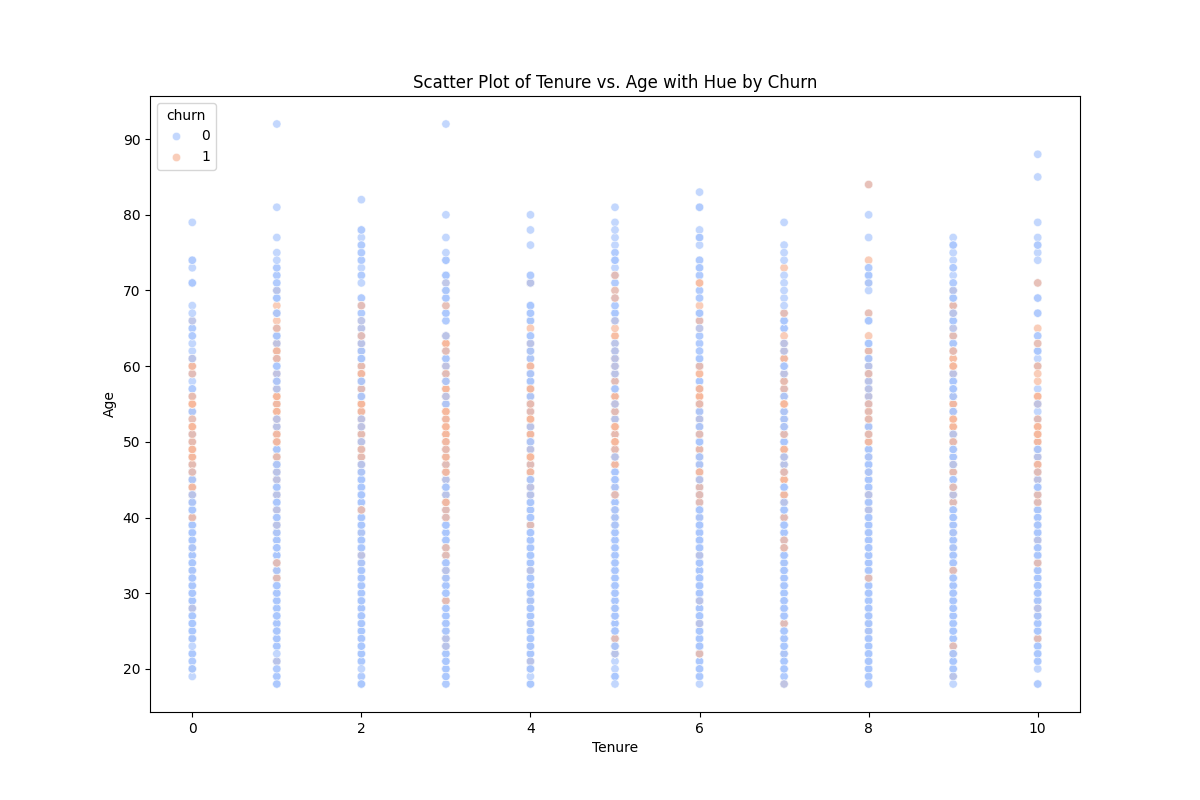
creditchurnvsnochurn
When pairing tenure with age, we can now see that those between the age of 40 and 65 are more likely to churn. This association persist through years of tenure with the bank. analysis of any longitudinal populations.








A quick way of objectively checking some of these associations is through a correllation matrix. 

					

# Heatmap for selected numerical variable correlations
plt.figure(figsize=(10, 8))
selected_numerical_cols = ['age', 'balance', 'products_number', 'estimated_salary']
selected_corr_matrix = df[selected_numerical_cols].corr()
sns.heatmap(selected_corr_matrix, annot=True, cmap='coolwarm')
plt.title('Correlation Matrix for Selected Numerical Variables')
plt.show()

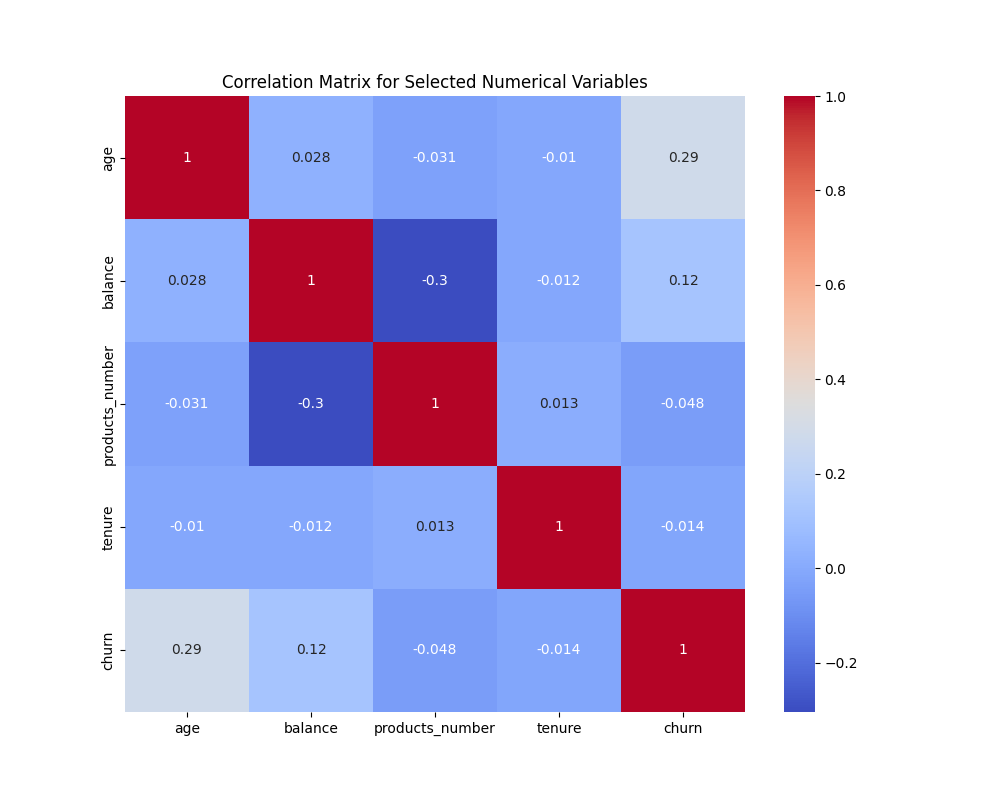
creditchurnvsnochurn
Of the selected variables, we can see that the previous trend of age increase being associated with churn is replicated in the correlation matrix.

Conclusion

Though brief, this analysis outlined several factors associated with increased bank customer attrition.

  1. Increased age of the customer was associated with churn, this remained true regardless of tenure.
  2. A worse credit score was associated with increased churn.
  3. Female customers were more likely to churn.
  4. Using more than 2 products had a much higher likelihood of churning.
// Initialize Prism Prism.highlightAll();